General Instructions to the Students

Remember that our purpose in thinking about this question is to help us (as a calculus learning community) better understand the essential concepts in calculus. Surprisingly, there are not many essential ideas in calculus so it is important that we all construct correct and meaningful understandings of what they are and how they work. Central to Calculus I is the notion of a function. This first question asks you to think about some particular functions.

Our goal, as a class, is to arrive at a correct and thoroughly explained answer to the posed question. Individually your goal should be to move the conversation, and our collective understanding forward. Your response to this question may take a variety of forms. You may want to suggest an answer to the question. You may want to offer a clarification of the meaning of a particular term or phrase. You may want to pose a thoughtful question whose answer might help you think about the original question in a different way. You may want to reply (with a question, correction, clarification or elaboration) to a response from another classmate. You may want to pose an interesting problem that bears some relationship to the original question. After reading the responses of your classmates, you may want to formulate a succinct synopsis. Regardless of the form it takes, your response should be clearly explained. Remember, you are writing to your classmates and you want your response to further their understanding.

In order to keep the conversation organized, we ask that you be very careful about threading your responses appropriately. If you are responding to the original question, click on instructor and reply. If, however, you are responding to a particular student, click on that student's response and reply. NEVER SELECT THE COMPOSE BUTTON IN THE MENU.

You are required to respond and your responses will be graded as high quality (response is clear & well thought out, moves the conversation forward - 20/20), average quality (response is understandable, keeps the conversation even - 15/20), low quality (response is vague, confuses the conversation - 10/20) or did not participate (0/20). High quality responses come in a variety of forms. Of course, we would like to see you answer the original question. However, we are also looking for good questions that emanate from the original question. You are welcome to respond more than once and your grade will be determined by the total contribution that you make to the final solution of the question. It goes without saying that all responses should be respectful of the ideas of others.

Instructions for Student Introductions

This website is shared by students in Calculus I (Sections A, B, C), Calculus II and Calculus III. Its primary purpose is to allow you to become involved in the community of calculus learners. Calculus Conversations is a place where you can ask questions or pose new problems. It is also a place where you can help answer questions and problems posed by your classmates. Together, we will work on categorizing the questions and problems, restating them in clear mathematical terms, and we will suggest strategies for finding solutions. In a small, but important way we will be working together towards a deeper understanding of how mathematical ideas can help us ask and answer interesting and important questions. To help us get to know each other better, we ask that you each reply to this message by posting a brief introduction of yourself. Let us know a little about why you are taking calculus, and share with us a few personal facts: where are you from? any hobbies? what do you want to be when you grow up? etc. Postings are DUE by class time Friday, September 10th.

Calculus Conversation Problem 1 (Author: Tom Banchoff)

Has there ever been a time in your life when your height in inches has equaled your weight in pounds? Mathematically explain your answer.

Exam Question Related to Problem 1

Let f(x) and g(x) be functions defined on the interval a <= x <= b. Additionally suppose that f(a) < g(b). Sketch the graphs of f(x) and g(x) on the interval [a,b] so that at all values of c between a and b, f(c) is not equal to g(c). (i.e., f and g do not cross). What condition must hold in order to guarantee that f(x) = g(x) for some value of x between a and b?

Calculus Conversation Problem 2

In the Jesuit spirit of becoming men and women for others, you have decided to take part in a 5-mile charity walk. You are told that refreshments will be handed out to all volunteer walkers as they pass the 2.5-mile marker. You decide to walk at a constant speed of 3 miles per hour, and to pass the time you also decide to track your distance from the 2.5-mile marker during the entire walk. (Note that whether the 2.5 mile marker is ahead of you or behind you, your distance from the marker is to be considered
non-negative.) At the INSTANT you pass by the 2.5-mile marker, what can you say about the rate at which your distance from the marker is changing relative to time?

Exam Question Related to Problem 2

Suppose that you are given the formula for a function f(t) and you have no idea how to calculate the derivative, f'(t). Describe how you could obtain a good approximation for the instantaneous rate of change of f(t) at t=5. Assume that you have available some technology which gives you full graphing and computing capabilities but not the ability to calculate derivatives. Please describe the process completely and in adequate detail.

Calculus Conversation Problem 3

Two industries, the Springfield Nuclear Power Plant and the Krusty Brand Burger Company, are being charged by the Environmental Protection Agency (EPA) with dumping unacceptable levels of toxic pollutants into Springfield Lake. Both industries are currently dumping toxic pollutants into the lake at the same rate. In order to meet EPA compliance standards, over the next twelve months both industries must reduce the rate at which they are dumping toxic pollutants in the lake by 30%. The presidents of Springfield Nuclear Power Plant and Krusty Brand Burger hire a single engineering firm to develop a compliance plan acceptable to both companies. The plan maps out a specific schedule of continual reduction in the toxic dumping rate over the entire twelvemonth period ending in the required 30% reduction in the dumping rate as specified by the EPA. The Krusty Brand Burger Company follows the plan as outlined by the engineering firm. The Springfield Nuclear Power Plant manages to stay on plan for the first three months. Because of equipment breakdowns and delays in getting replacement parts, during the next three months the reduction rate achieved during the first three months is reversed, and at the end of the first six-months, the Springfield Nuclear Power Plant dumping rate is back to where it was in the beginning. Once the equipment is repaired, the industry uses extra resources to continually reduce the dumping rate, and over the remaining six months the company manages to meet the30% reduction in the dumping rate set by the EPA. COMPLETELY DESCRIBE the graphs of each company's individual contribution to the total level of toxic pollutants in the lake as a function of time over the twelve-month EPA observation. Has either industry been a better environmental citizen? Mathematically explain your answer.

Exam Question Related to Problem 3

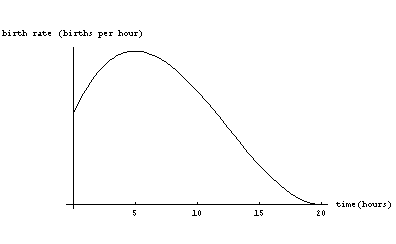
Consider a bacteria population whose birth rate changes in the following ways during a twenty-hour period:

· The birth remains nonnegative (i.e., positive or zero) during the entire twenty hour period.
· The birth rate begins the twenty-hour period at a positive value.
· During the first five hours, the birth rate continually increases and reaches a maximum value at the end of five hours.
· During the next fifteen hours, the birth rate continually decreases, reaching a level of zero right at the end of the twenty-hour period.

The graph of the birthrate as a function of time in hours is shown below for this twenty hour period. The birth rate is in given in births per hour.

Explain what the birth rate curve tells you about the total number of individuals born (during the twenty-hour period) by time t. Does the graph of the total number born by time t have an inflection point during the twenty-hour period? If so, at what time (within the twenty-hour period) does it occur? Sketch the graph of the total number of individuals born (during the twenty-hour period) by time t.