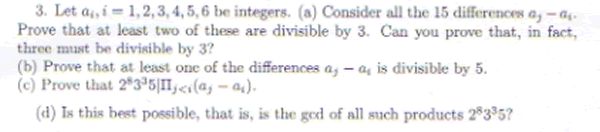
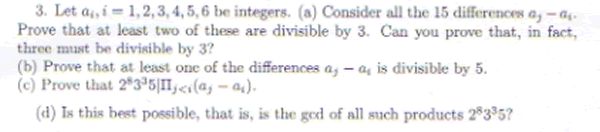
Discussion: This problem makes use of the unique factorization and the pigeonhole principle. For example, there are three classes that an integer can be in modulo 3. If any class contains three of the numbers then then the three differences of two of them are all divisible by 3. Alternatively, if each class contains two numbers then each of those differences is divisible by three. Parts b) and c) are proved similarly. The student does not show that this is best possible, though taking the six integers to be 1,2, . . . , 6 yields exactly the given number.

Click the image to the left to bring up an enlarged copy of this student's solution.